Introduction

[justify]The current articles on the website have talked about how to hide data inside images via either appending bytes after an image and by manipulating pixels. In this article, were going to go a bit deeper in the second technique by explaining a few algorithms used to hide data.[/justify]

Knowledge that will help you to read this article:

Well consider the following:

Brief explanation of image architecture

[justify]Here is what you should keep in mind: an image file is not more than a huge list of pixels that should be displayed on your screen.
In a 24bpp BMP file, we can distinguish two main parts; a header thats describing the file and a body thats including all the pixel information.
A pixel is a composition of 3 colors, red, green and blue that are encoded in 1 byte per color (so 3 for a pixel). A byte can take value from 0 to 255 and its those byte we will alter to hide our data.[/justify]

Methods of hiding data

Method 1: Encode raw bytes

[justify]This method consists of encoding each value as they are inside our image.
Lets say we want to hide the word Hidden inside an image. Thats 6 characters to hide (so 6 bytes). Since we can hide 3 bytes per pixels, thats means we can hide our data in 2 pixels.

Lets create an image with a width of 2 and height of 1.
[/justify]

We want to put our data so we can hide Hid in the first pixel and den in the second one:

Lets transform our data into its hexadecimal representation.

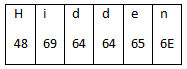
Were now able to affect value to our pixels:
Pixel 1: Red = 48 | Green = 69 | Blue = 64
Pixel 2: Red = 64 | Green = 65 | Blue = 6E

Congrats weve hidden our first data in an image!

Pros:

Cons:

[justify]Because of the cons we need to find a more reliable way to hide data without telling to everyone Hey! Look at my pixelated image, there is something here. If we cannot hide our data directly, why not just hide the minimum of information per pixels? As we said before, a pixel is 3 bytes that does take the value from 0 to 255. As a human, were not able to make the difference between a red with the value of 255 and the value of 254. Thats what were going to exploit to hide our data.[/justify]

Method 2: Least significant bit encoding

Were going to hide our data by using only the least significant bits of a pixel. That means we can use up to 3 bits per pixels. Lets take the word Hidden again and hide it with this method. We still have 6 bytes to hides but since one byte contains 8 bits and we cannot store more than 3 bits per pixels well need a bigger image if we want be able to hide this data.

Lets calculate the space well need this time:
6bytes * 8bits = 48 bits to hide.
48 bits / 3bits per pixel = 16 pixels.
Thats 800% more pixels than the first method!

Lets then make an image with a width of 4 and an height of 4 and add a white background. Now, lets transit our data into 8 bits padded binary:

We need to encode this data into each pixel we have. Since we have a white image, all the pixels have the hex value of FF FF FF thats 11111111 11111111 11111111 in binary. To hide the letter H, well need approximately 3 pixels. So lets change the pixels composite by the following:

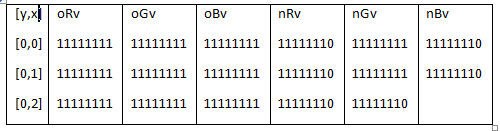
Repeat this for each byte in our data and were now having a data hidden that is invisible to human eyes!

Pros:

Cons:

[justify]Now weve find a way to make our change invisible, the truth is the human eye is even less perfect than that and were going to optimized our method with this.
It has been proved that the human eyes can only percept about 10 millions of colors.
Thus said, we can calculate how many bits we are able to change to keep our changes invisible.
Well be quick and admit we can modify at most 5 bits. Since our eyes are more sensitive to contrast change on the green channel, well only modify 1bit from here and 2 from the others.
Here come the third method[/justify]

Method 3: least significant bit encoding (optimized)

[justify]So far, this method is the same as the second one, but instead of storing only 3 bit per pixel, well store 5. Thats ensuring ~ 1.7 pixels per character.
In our case and the hiding of the word Hidden it will be still +480% spaces occupied than the first method but much compressed than the second one.

Lets see for example what will looks like the letter H inside our white image.
H = 01001000 =>
[/justify]

Process the same for each character to hide and youre done.

Pros:

Cons:

Improvements

We got out way to hide data but now a few problems persist.
Here is some and how we can possibly fix them:

How to know the length of the data?

Lets say we have a recalcitrant mailbox thats filter any exe were sending even inside archive and it pissed us off so much that weve decided to hide it into a photo of our cat (because there is not enough over the net).
So far, for a text based data thats fine, youll be able to see by yourself where it starts and where its end.
But for the case of an executable, thats another story !
We must know how many data we need to extract or well never get our exe to work.

Example: Write an Header
We can write an header with the seize of the data to recover. Lets take a 32 bits integer so we can reserve little less than 7 pixels to write the length of our data.
If we want apply this to our word Hidden with the method 3, this will be:
Length(Hidden) = 6 = 110 = 00000000 00000000 00000000 00000110
Lets just prefix this value to our image and well have the length of the data to extract.

How to prevent an attacker from extracting our data?

Hard time here, we spend so much time encoding our data but theyre still so easy to read. No doubt someone suspicious fill find out whats going on if he intercept our images. The first one will probably be to add offset to our data so we can hide them in a specific area of our image. This is not an acceptable solution as a global analysis will just break it. Instead, were going to generate a key that will contain all the pixel indexes where we can find our data. Lets say we want to hide the word Hide into a 5w * 5h image. We need to generate a key of the position of 7 pixels.

For example:

=> 14, 8, 15, 1, 3, 9, 5  

Well be hiding the 5 first bit of h in the pixel n¹⁴ and the 3 other in the pixel n⁸ then the first two bits of I in the pixel 8, 5 other in pixel n¹⁵ and the last one in n¹ etc..

For better results, well use a cryptographic random to generate the key. We even can improve this by setting the number of bits were hiding from 1 to 5 and make the output even less predictable but we need make sure our image can support the amount of data were going to store with the specified key.

Please note this is not a perfect solution to hide data and it shouldnt be used as it is for real critical information.